Zheng-Meng Zhai

Zheng-Meng Zhai

Ph.D. student at Arizona State University

Research

$\color{Blue}{\textsf{Reservoir computing}}$

Reservoir computing (RC) is a type of recurrent neural networks (RNNs). It trains only the readout weights using linear regression, leaving the input weights and recurrent connection weights untrained. This approach gives RC a notable advantage over other RNNs, particularly in terms of rapid learning.

We have applied reservoir computing to tackle a range of challenges in nonlinear systems, including tracking control, magnetic navigation, AMOC prediction, and parameter tracking, among other applications.

Relevant Publications:


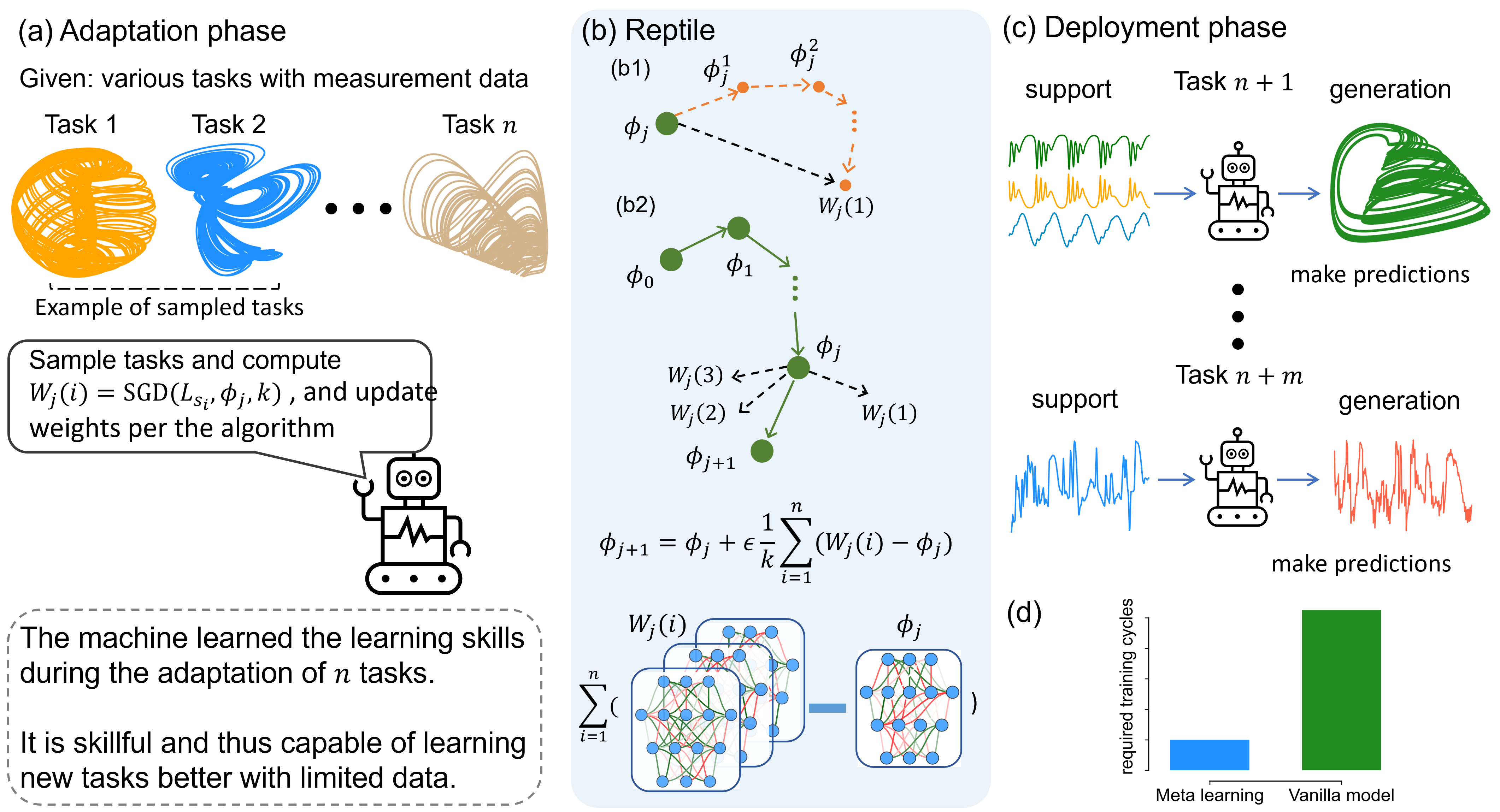
$\color{Blue}{\textsf{Meta-learning with dynamical systems}}$

How can reliable dynamics be learned when only very limited data are available?

We develop a meta-learning framework that leverages synthetic chaotic systems to “learn how to learn” complex dynamics. During the adaptation phase, the model gathers experience from diverse synthetic systems. In the deployment phase, it rapidly reconstructs the dynamical climate of new ecological systems using only limited data. Benchmark population models and real-world datasets in ecological are used to validate.

Relevant Publications:


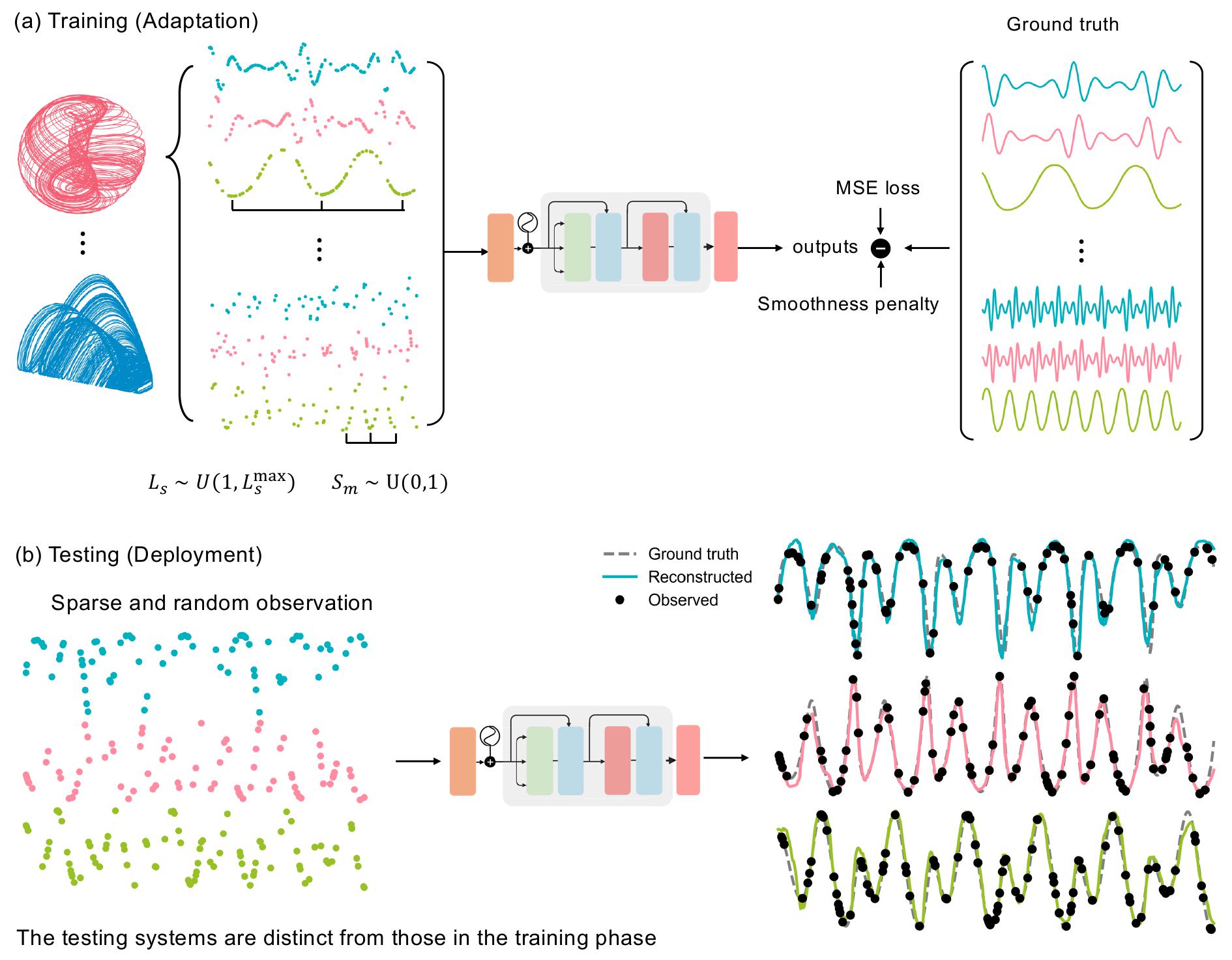
$\color{Blue}{\textsf{Zero-shot dynamics reconstruction}}$

Can the dynamics be faithfully reconstructed from the limited observations without any training data?

We develop a hybrid transformer and reservoir-computing machine-learning scheme. A number of known chaotic systems are used to train the transformer, during which the target systems are never exposed to it. In testing, the sparse data from the new unseen target system is provided to the well-trained transformer to recover its dynamics. In experiments on unseen target systems with high sparisty observations, the model can still reconstruct the dynamics.

Relevant Publications:


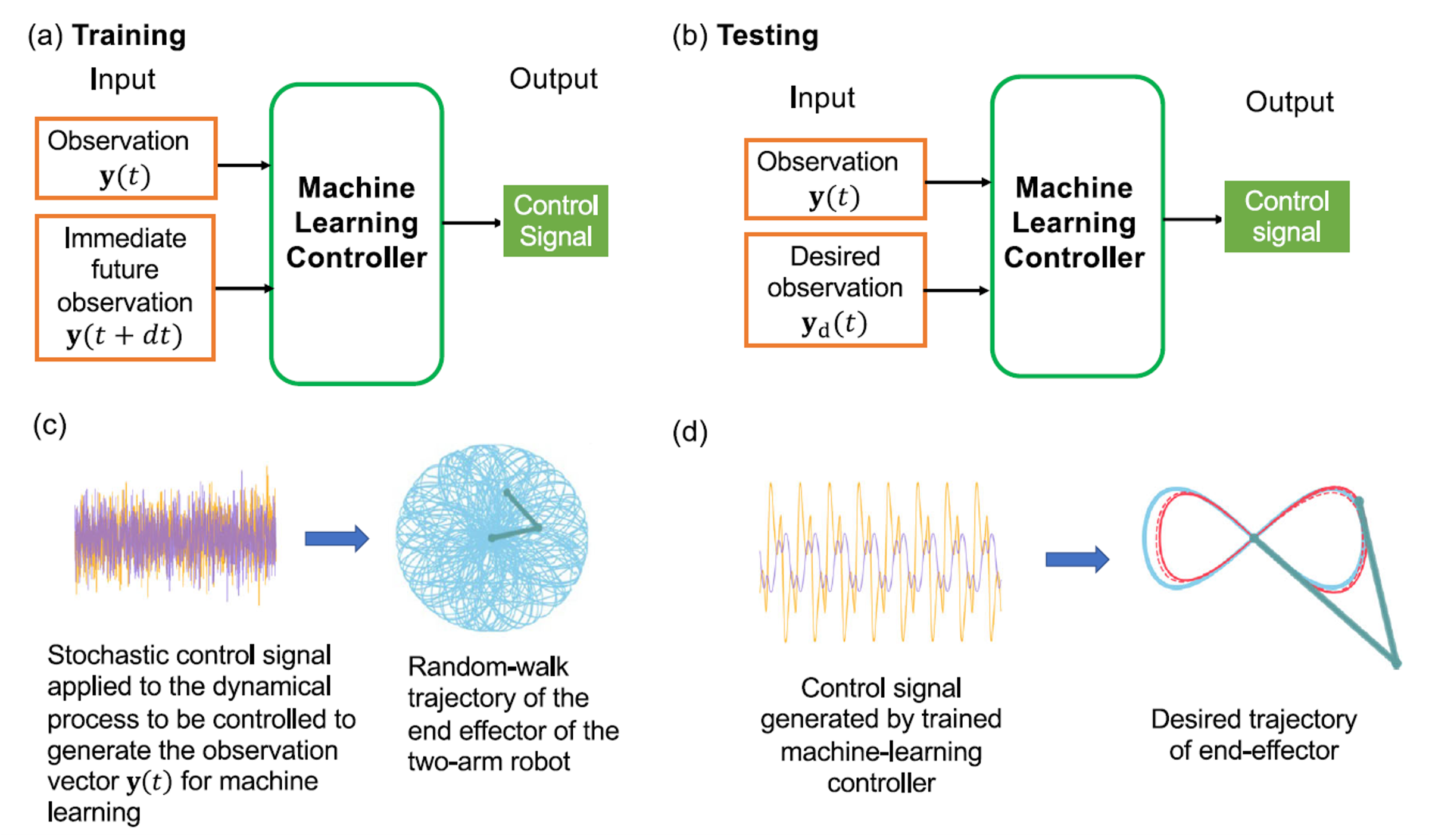
$\color{Blue}{\textsf{Tracking control with machine learning}}$

A model-free, machine-learning framework is developed to control a two-arm robotic manipulator using only partially observed states, where the controller is realized by reservoir computing.

Stochastic input is exploited for training. By so doing, the model trained on ‘‘random-walk’’ like signals is effective on tracking a variety of periodic and chaotic signals.

Relevant Publications:


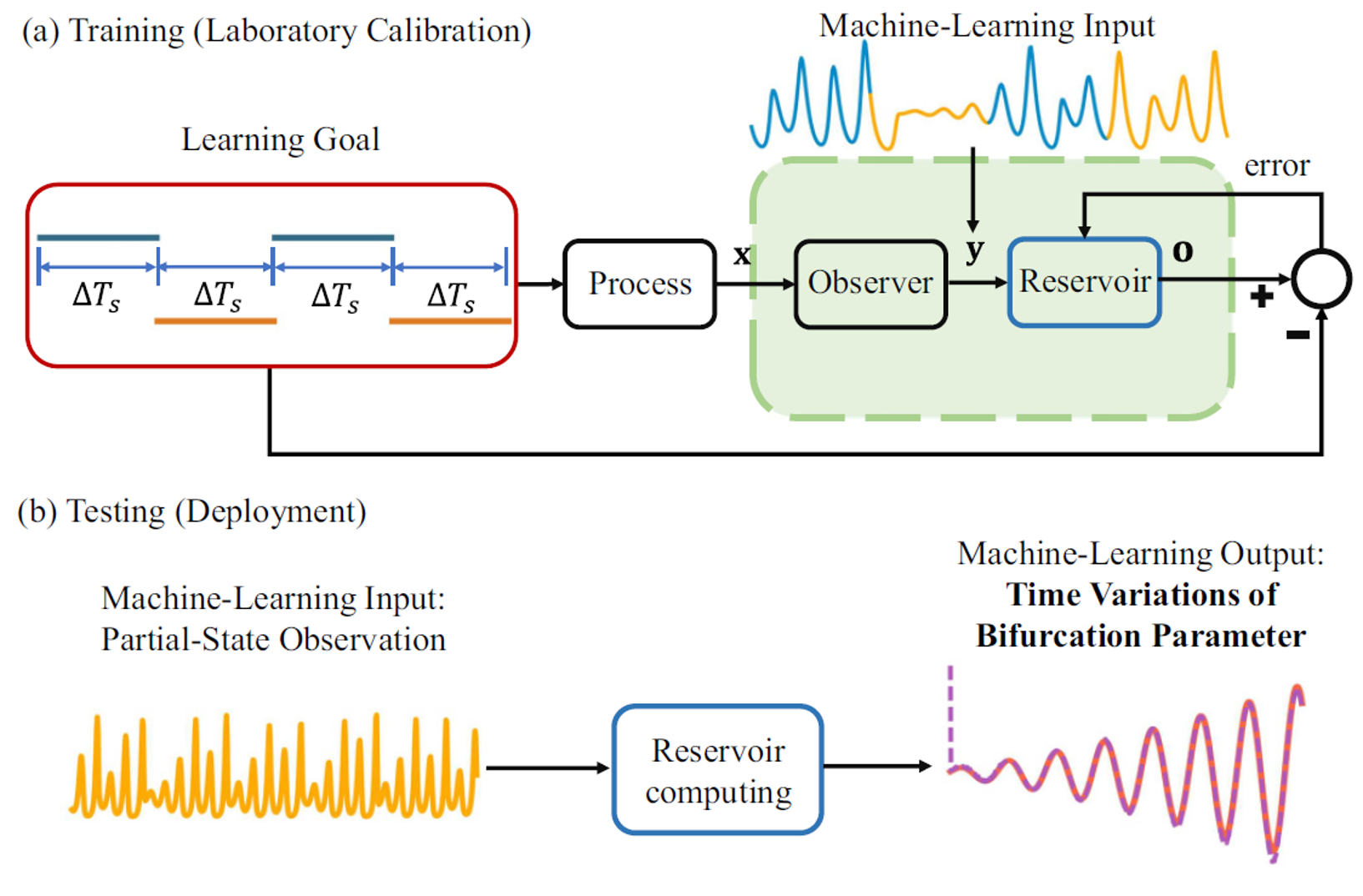
$\color{Blue}{\textsf{Inverse model meets machine learning}}$

Inverse modeling contrasts with direct modeling by working backwards from outcomes to infer unknown inputs or system characteristics.

we train a reservoir computer using constant parameters obtainable in a laboratory setting and their corresponding partial observations. During deployment, this reservoir computer tracks time-varying parameters using partial state observations, though the ground truth is no longer accessible. This idea is similarly applicable in nonlinear tracking control, where the input comprises both current and desired partial state observations, and the output generates the necessary control signals.

Relevant Publications:


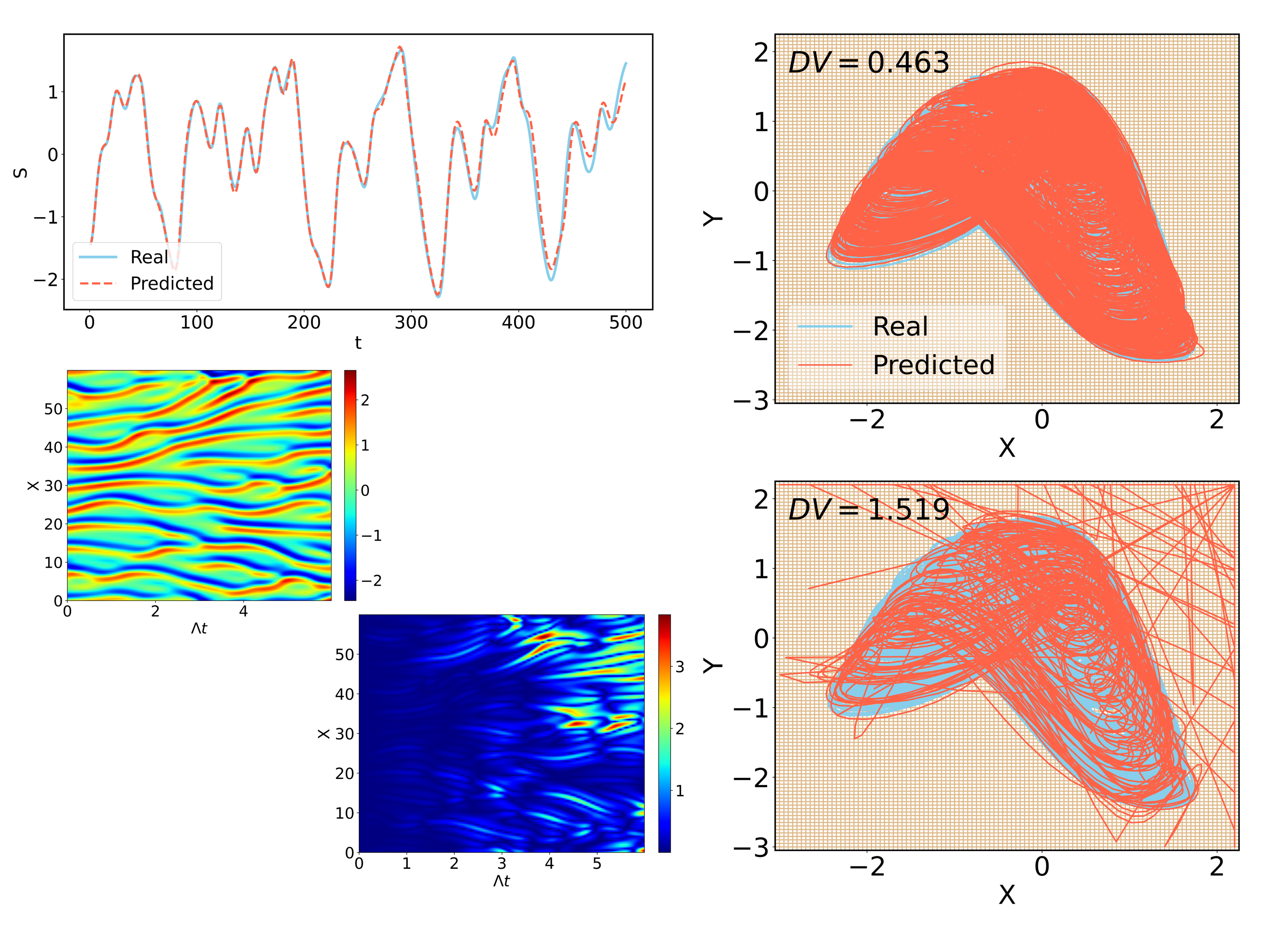
$\color{Blue}{\textsf{Chaotic systems short- and long-term prediction}}$

The chaotic systems can be predicted of the state variables in-short term and attractor reonstruction in long-term.

We have utilized reservoir computing to predict the behavior of chaotic systems, including the Lorenz, Mackey-Glass, and Kuramoto-Sivashinsky systems, and so on, over both short and long terms. Our studies reveal that introducing an optimal level of noise enhances performance, a phenomenon we describe as stochastic resonance.

Relevant Publications: